| Classwise Concept with Examples | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Construction of a Line Parallel to a Given Line through a Point not on it | Construction of Triangles | |
Chapter 10 Practical Geometry (Concepts)
Transitioning from the theoretical exploration of geometric shapes and their properties, this chapter delves into the realm of Practical Geometry. Here, the primary focus shifts towards the methodical and precise construction of various geometric figures using a specific, limited set of tools: primarily an unmarked ruler (or straightedge) and a pair of compasses. The emphasis is placed squarely on accuracy, logical sequencing of steps derived directly from established geometric theorems and properties, and the ability to replicate shapes based on given parameters. This hands-on approach solidifies theoretical understanding through tangible application.
We commence by addressing fundamental constructions, such as drawing a line parallel to a given line. This might involve constructing a parallel line that passes through a specific point not situated on the original line, or constructing one at a predetermined perpendicular distance. These initial constructions often rely heavily on the principles governing angles formed by parallel lines and a transversal, specifically by meticulously creating arcs and intersections to ensure either equal corresponding angles or equal alternate interior angles. This process serves as an immediate practical reinforcement of the concepts explored theoretically in the study of lines and angles, demonstrating how abstract properties guide physical creation.
The core of this chapter, however, is dedicated to the detailed construction of triangles based on specific sets of given measurements. These sets of conditions correspond directly to the congruence criteria previously studied (SSS, SAS, ASA, RHS), providing tangible proof that these minimal conditions are indeed sufficient to define a unique triangle (up to congruence). Students will master the step-by-step procedures for constructing triangles under various scenarios:
- SSS Criterion (Side-Side-Side): Constructing a triangle when the lengths of all three sides are provided. This involves drawing a base side and then using the compasses, set to the lengths of the other two sides, to draw arcs from the endpoints of the base. The intersection of these arcs determines the third vertex.
- SAS Criterion (Side-Angle-Side): Constructing a triangle when the lengths of two sides and the measure of the included angle (the angle formed between these two sides) are known. Typically, one side is drawn, the specified angle ($e.g., 60^\circ, 90^\circ$, often constructible with compasses, or using a protractor if permitted) is constructed at one endpoint, and the second side's length is marked off along the new arm of the angle using the compasses.
- ASA Criterion (Angle-Side-Angle): Constructing a triangle given the measures of two angles and the length of the included side (the side positioned between these two angles). The construction starts by drawing the included side, then constructing the two specified angles at its endpoints. The point where the non-common arms of these angles intersect forms the third vertex.
- RHS Criterion (Right angle-Hypotenuse-Side): Specifically for constructing a right-angled triangle when the length of the hypotenuse and the length of one other side (a leg) are given. This usually involves drawing a line, constructing a perpendicular ($90^\circ$ angle) to create the right angle, marking off the length of the given leg, and then using the compasses set to the hypotenuse length to draw an arc from the end of the leg to intersect the base line, thus locating the third vertex.
Underpinning all these constructions is the fundamental geometric principle that each of these specific sets of conditions (SSS, SAS, ASA, RHS) uniquely determines the size and shape of a triangle. The process emphasizes the importance of preliminary planning, strongly encouraging the practice of drawing a quick rough sketch before commencing the precise construction. This sketch helps visualize the steps and the final figure. Accurate labeling of vertices, sides, and angles on the final, precise construction is also crucial. Through these exercises, students develop enhanced spatial reasoning, cultivate meticulousness and precision in their work, and gain a deeper, more intuitive understanding of geometric properties and the powerful concept of congruence.
Construction of a Line Parallel to a Given Line through a Point not on it
In the previous chapter on Lines and Angles, we learned about parallel lines and the special angle relationships created when a transversal line intersects them (corresponding angles, alternate interior angles, etc.). We also saw that if certain angle conditions are met (like alternate interior angles being equal), then the two lines are parallel. In practical geometry, we use these properties to construct parallel lines accurately using compass and ruler.
A common construction problem is to draw a line that is parallel to a given line and passes through a specific point that is not located on the given line.
Method using Alternate Interior Angles
We can construct a parallel line by using the property that if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the lines are parallel. The construction involves copying an angle at a different position to create a pair of equal alternate interior angles.
Given:
A straight line $l$ and a point $A$ that is not on the line $l$.

Construction Required:
To construct a new straight line, let's call it $m$, such that line $m$ passes through the point $A$ and is parallel to the given line $l$ ($m \parallel l$).
Steps of Construction:
Follow these steps using a ruler (as a straightedge) and a compass:
- Step 1: Draw a Transversal
Take any point $B$ on the given line $l$. Join point $A$ to point $B$ with a straight line segment using a ruler. The line segment AB will act as a transversal cutting line $l$.
- Step 2: Draw an Arc at the Known Angle
With $B$ as the center, choose a convenient radius for your compass. Draw an arc that intersects the line $l$ at a point, say $C$, and also intersects the line segment $AB$ at another point, say $D$. This arc marks the angle $\angle CBD$ (or $\angle ABC$) that we will copy.
- Step 3: Draw an Arc at the New Vertex
Now, with $A$ as the center and using the exact same radius that you used in Step 2, draw another large arc. This arc should cut the line segment $AB$ at a point, say $G$, and should extend towards the side where the parallel line will be drawn.
- Step 4: Measure the Width of the Original Angle
Place the compass needle at point $C$ (where the first arc intersected line $l$) and adjust the compass opening so that the pencil tip is exactly at point $D$ (where the first arc intersected segment $AB$). This sets the compass opening equal to the chord length of the arc CD, effectively measuring the angle's opening.
- Step 5: Mark the Copied Angle's Width
Keeping the compass opening from Step 4, place the compass needle at point $G$ (the point where the second arc intersected AB). Draw a small arc to cut the large arc you drew in Step 3. Label this intersection point $H$.
- Step 6: Draw the Parallel Line
Draw a straight line passing through the point $A$ and the new intersection point $H$ using a ruler. Extend this line on both sides. Label this line $m$.


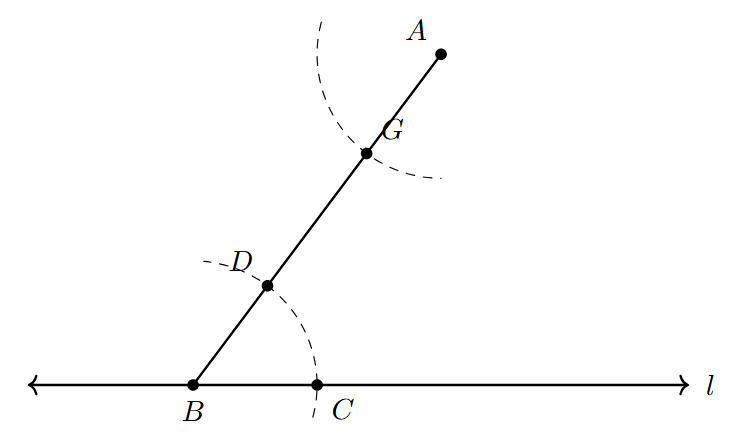


The line $m$ that you have drawn passes through point $A$ and is parallel to the given line $l$.
Justification:
By construction, we have copied $\angle CBD$ to the position of $\angle GAH$.
The arcs were drawn with the same radius ($BD = AG$). The chord lengths were also made equal ($CD = GH$). This ensures that the angles they subtend are equal.
$\angle GAH = \angle CBD$
(By construction)
We can see that $\angle GAH$ and $\angle CBD$ (which is the same as $\angle ABC$) are a pair of alternate interior angles with respect to the lines $l$ and $m$ and the transversal $AB$.
According to the converse of the Alternate Interior Angles Theorem, if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.
Therefore, Line $m \parallel$ Line $l$.
Since line $m$ also passes through point $A$ (by construction), it is the required parallel line.
Construction of Triangles
A triangle is a fundamental geometric shape defined by three sides and three angles. While every triangle has these six elements, we do not need to know the measures of all six elements to construct a unique triangle. In fact, knowing certain minimum combinations of sides and angles is enough to construct one and only one triangle. These minimum conditions are related to the congruence criteria we studied in the previous chapter.
Conditions for Unique Triangle Construction
In practical geometry, constructing a "unique" triangle means drawing one and only one triangle with the given measurements. If the given measurements satisfy one of the congruence criteria, then any triangle constructed with those measurements will be congruent to any other triangle constructed with the same measurements. The key congruence criteria we can use as construction conditions are:
1. SSS Criterion (Side-Side-Side): If the lengths of the three sides of a triangle are given, a unique triangle can be constructed (provided the triangle inequality holds). This corresponds to the SSS congruence rule.
2. SAS Criterion (Side-Angle-Side): If the lengths of two sides and the measure of the angle included between these two sides are given, a unique triangle can be constructed. This corresponds to the SAS congruence rule.
3. ASA Criterion (Angle-Side-Angle): If the measures of two angles and the length of the side included between these two angles are given, a unique triangle can be constructed. This corresponds to the ASA congruence rule.
4. RHS Criterion (Right angle-Hypotenuse-Side): For a right-angled triangle, if the length of the hypotenuse and the length of one leg (side) are given, a unique right-angled triangle can be constructed. This corresponds to the RHS congruence rule.
Example. Construct a triangle ABC with the following dimensions: $AB = 5$ cm, $BC = 7$ cm, and $AC = 6$ cm.
Given:
The lengths of the three sides of $\triangle ABC$ are $AB = 5$ cm, $BC = 7$ cm, and $AC = 6$ cm.
To Construct:
A triangle $\triangle ABC$ with the given dimensions.
First, we check the Triangle Inequality Condition:
- $AB + AC > BC \implies 5 + 6 = 11 > 7$ (True)
- $AB + BC > AC \implies 5 + 7 = 12 > 6$ (True)
- $AC + BC > AB \implies 6 + 7 = 13 > 5$ (True)
Since the sum of any two sides is greater than the third side, a triangle with these dimensions can be constructed.
Steps of Construction:
Step 1: Draw a line segment BC of length 7 cm. This will be the base of the triangle.

Step 2: With B as the center and a radius of 5 cm (the length of AB), use a compass to draw an arc.

Step 3: With C as the center and a radius of 6 cm (the length of AC), draw another arc that intersects the first arc.
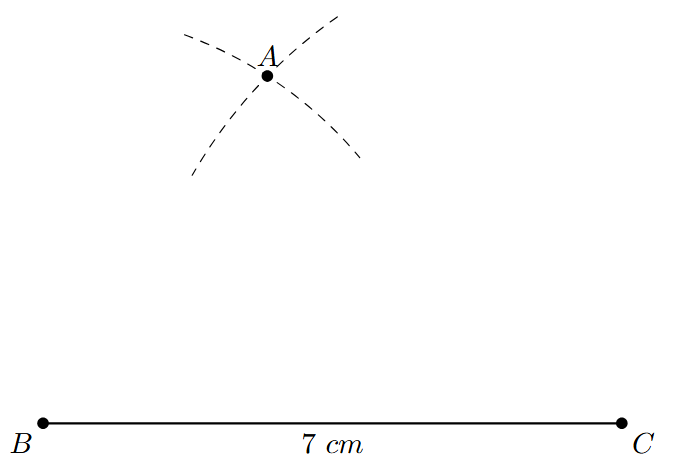
Step 4: Label the point of intersection of the two arcs as A.
Step 5: Join A to B and A to C using a ruler to form the line segments AB and AC.

The resulting $\triangle ABC$ is the required triangle with sides $AB = 5$ cm, $BC = 7$ cm, and $AC = 6$ cm.
Construction based on SAS Criterion
This criterion applies when the lengths of two sides and the measure of the angle included between them are known. This information is sufficient to construct a unique triangle.
Example. Construct a triangle PQR where $PQ = 5.5$ cm, $QR = 6.5$ cm, and the included angle $\angle PQR = 75^\circ$.
Given:
The lengths of two sides of $\triangle PQR$ are $PQ = 5.5$ cm and $QR = 6.5$ cm.
The measure of the included angle is $\angle PQR = 75^\circ$.
To Construct:
A triangle $\triangle PQR$ with the given dimensions.
Steps of Construction:
Step 1: Draw a line segment QR of length 6.5 cm using a ruler. This will serve as the base of the triangle.

Step 2: At point Q, construct an angle of $75^\circ$ using a protractor. Let the ray originating from Q be QX. So, $\angle RQX = 75^\circ$. (Note: A $75^\circ$ angle can also be constructed with a compass by bisecting the angle between $60^\circ$ and $90^\circ$).

Step 3: With Q as the center and a radius of 5.5 cm (the length of PQ), use a compass to draw an arc that intersects the ray QX.
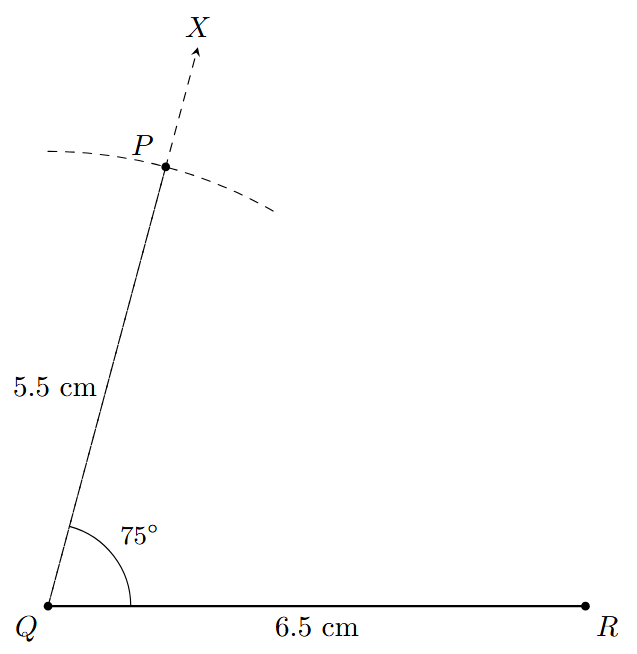
Step 4: Mark the point of intersection as P. This point is 5.5 cm away from Q along the ray that makes a $75^\circ$ angle with QR.
Step 5: Join P to R with a straight line segment using a ruler to complete the triangle.

The resulting $\triangle PQR$ is the required triangle with sides $PQ = 5.5$ cm, $QR = 6.5$ cm, and the included angle $\angle PQR = 75^\circ$.
Construction based on ASA Criterion
Example. Construct a triangle DEF where the included side $DE = 7$ cm, and the angles at its endpoints are $\angle FDE = 40^\circ$ and $\angle FED = 60^\circ$.
Given:
The length of the included side of $\triangle DEF$ is $DE = 7$ cm.
The measures of the two angles are $\angle FDE = 40^\circ$ and $\angle FED = 60^\circ$.
To Construct:
A triangle $\triangle DEF$ with the given dimensions.
First, we check if a triangle is possible. The sum of the given angles is $40^\circ + 60^\circ = 100^\circ$. Since this sum is less than $180^\circ$, a triangle can be formed.
Steps of Construction:
Step 1: Using a ruler, draw a line segment DE of length 7 cm. This forms the included side of the triangle.

Step 2: Place the center of a protractor at point D and align its baseline with the segment DE. Mark an angle of $40^\circ$ and draw a ray starting from D, let's call it DX. So, $\angle EDX = 40^\circ$.
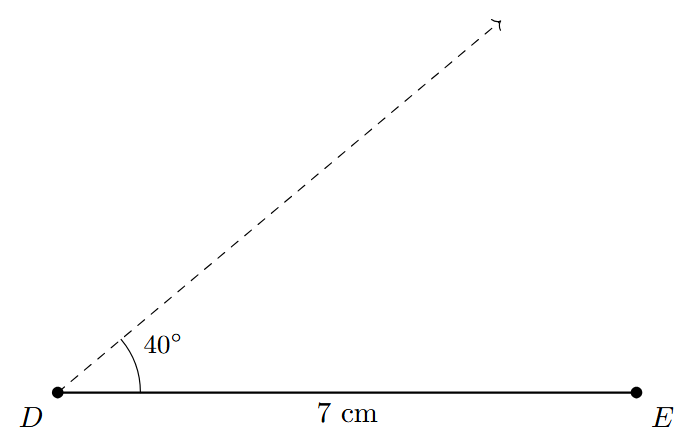
Step 3: Place the center of the protractor at point E and align its baseline with the segment DE. Mark an angle of $60^\circ$ and draw a ray starting from E, let's call it EY. So, $\angle DEY = 60^\circ$.
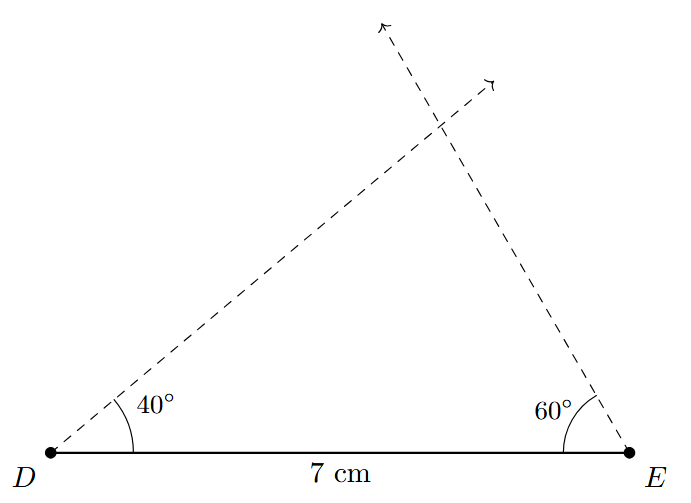
Step 4: The two rays, DX and EY, will intersect at a single point. Label this point of intersection as F.
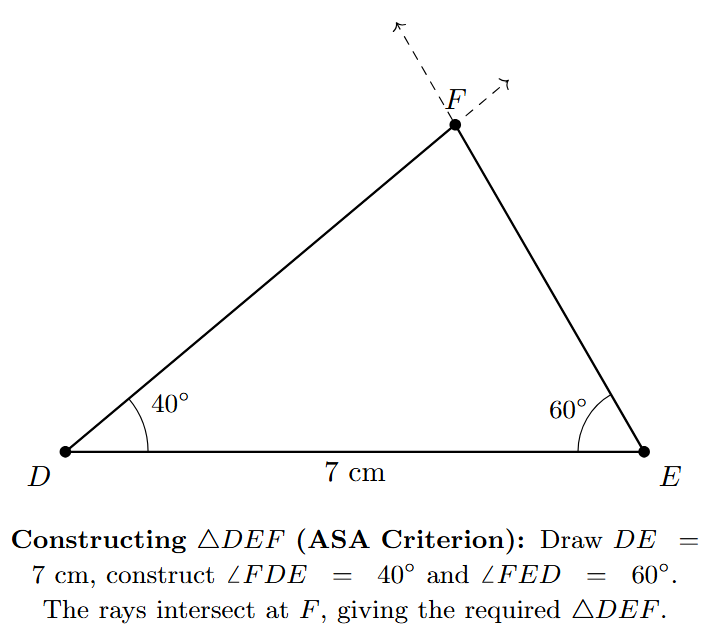
The resulting $\triangle DEF$ is the required triangle with side $DE = 7$ cm, $\angle FDE = 40^\circ$, and $\angle FED = 60^\circ$.
Construction based on RHS Criterion
Example. Construct a right-angled triangle LMN, where the right angle is at M, the hypotenuse LN = 5 cm, and one leg MN = 3 cm.
Given:
In $\triangle LMN$:
- The angle at M is a right angle, i.e., $\angle LMN = 90^\circ$.
- The length of the leg MN is 3 cm.
- The length of the hypotenuse LN is 5 cm.
To Construct:
A right-angled triangle $\triangle LMN$ with the given dimensions.
Steps of Construction:
Step 1: Draw a line segment MN of length 3 cm using a ruler. This is the given leg of the triangle.
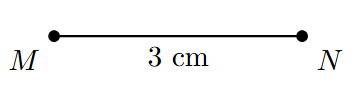
Step 2: At point M, construct a perpendicular line or a ray MX to the segment MN, such that $\angle NMX = 90^\circ$. This can be done using a protractor or a compass and ruler.

Step 3: With N as the center and a radius of 5 cm (the length of the hypotenuse), use a compass to draw an arc that intersects the ray MX.

Step 4: Mark the point of intersection of the arc and the ray MX as L. This is the third vertex of the triangle.
Step 5: Join L to N with a straight line segment using a ruler to complete the triangle.

The resulting $\triangle LMN$ is the required right-angled triangle with $\angle M = 90^\circ$, $MN = 3$ cm, and $LN = 5$ cm.
Why AAA is Not a Criterion for Unique Triangle Construction
We have seen that knowing SSS, SAS, ASA, or RHS is sufficient to construct a unique triangle. However, if we are only given the measures of the three angles of a triangle (AAA - Angle-Angle-Angle), we cannot construct a unique triangle. We can construct many triangles that have the same angle measures but are of different sizes.
Reason: Consider the case where we are asked to construct a triangle with angles $60^\circ, 60^\circ,$ and $60^\circ$. We know this describes an equilateral triangle. We can draw an equilateral triangle with side length 2 cm. All its angles will be $60^\circ$. We can also draw an equilateral triangle with side length 3 cm, or 4 cm, or any other positive length. All these triangles will have angle measures $60^\circ, 60^\circ, 60^\circ$, but their side lengths and overall sizes will be different.
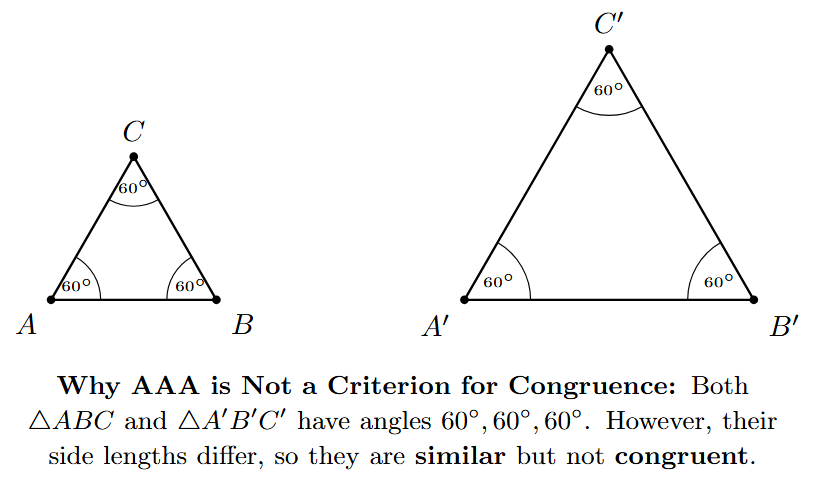
Triangles that have the same shape (same angle measures) but are of different sizes are called similar triangles. AAA is a criterion for similarity, but it is not a criterion for congruence (which requires both the same shape *and* the same size). Therefore, knowing only the angles does not uniquely determine the triangle's size.

